Algorithms and complexity results for finding graphs with extremal Randić index
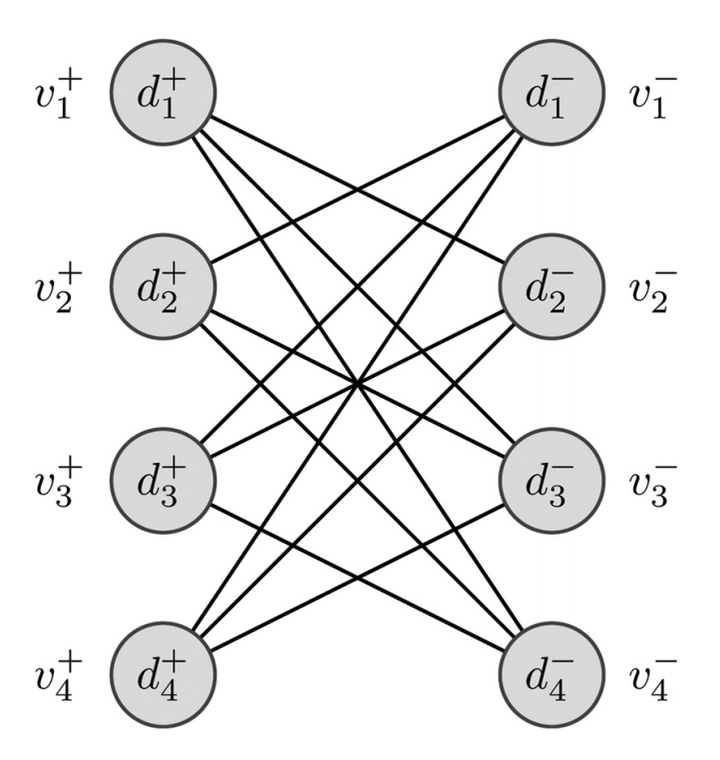Bipartite setup of the generalized Randić index degree sequence problem for an example directed graph.
Abstract
We show that finding a subgraph realization with the minimum generalized Randić index for a given base graph and degree sequence is solvable in polynomial time by formulating the problem as the minimum weight perfect b-matching problem of Edmonds (J Res Natl Bur Stand 69B (1965), 125–130). However, the realization found via this reduction is not guaranteed to be connected. Approximating the minimum weight perfect b-matching problem subject to a connectivity constraint is shown to be NP-hard. For instances in which the optimal solution to the minimum Randić index problem is not connected, we describe a heuristic to connect the graph using pairwise edge exchanges that preserves the degree sequence. Although we focus on finding graph realizations with minimum Randić index, our results extend to finding graph realizations with maximum Randić index as well. Applications of the Randić index are provided to synchronization of neuronal networks controlling respiration in mammals and to normalizing cortical thickness networks in diagnosing individuals with dementia.